Wenn im Zusammenhang mit Simulationen von Modellen gesprochen wird, handelt es sich in der Regel um mathematische Modelle. Dabei versteht man unter einem mathematischen Modell eine adäquate Beschreibung der in einem zu simulierendem System ablaufenden Vorgänge mit Hilfe mathematischer Methoden. Es besteht aus einer oder mehreren Gleichungen oder Ungleichungen, oder einer logischen und quantitativen Darstellung der Zusammenhänge zwischen den Variablen des Systems (Berghoff 1976). Der interne Aufbau eines Modells wird dabei durch die Festlegung des Zwecks, dem das Modell dienen soll, den verfügbaren Daten und sicherlich auch den spezifischen Kenntnissen und Neigungen des Modellierers bestimmt (Poethke 1994). Der erste Schritt beim Entwurf eines Modells ist im Allgemeinen ein Konzept. Es beschreibt die Zusammenhänge des zu simulierenden Systems, die entweder aufgrund von Versuchen gewonnen wurden oder aus anderen Quellen stammen, z.B. der Literatur. Dieses Konzept, im weiteren konzeptionelles Modell genannt, muß als nächstes in ein mathematisches Modell übertragen werden. Für Simulationen in der Ökologie heißt das, daß die internen Zusammenhänge, wie zum Beispiel die Lebensdaten und Wechselwirkungen mit anderen Arten der vorhandenen Organismen, bekannt sein müssen, ebenso wie ihre Abhängigkeit von abiotischen Bedingungen. Ohne diese Kenntnisse läßt sich kein konzeptionelles Modell formulieren. Liegen für einige Bereiche keine gesicherten Werte vor, so muß ein Wert oder ein Verhalten angenommen bzw. geschätzt werden.
Modelle sind somit immer nur eine Näherung an das reale Ökosystem, da es sich in seiner Komplexität nicht bis ins kleinste Detail nachbilden läßt. Somit müssen für eine Simulation diverse mehr oder weniger starke Vereinfachungen und Abstraktionen gemacht werden. Dabei zeigt sich, daß mit der Genauigkeit einer Simulation auch die Anforderungen an das Rechnersystem steigen, insbesonders an den Speicherbedarf und die Rechenzeit.
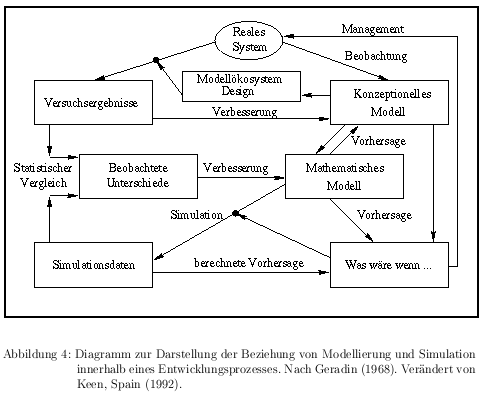
Ist für das zu simulierende Modellökosystem ein mathematisches Modell entwickelt worden, muß daraus ein Simulationsmodell erstellt werden. Das heißt, die mathematisch-logischen Formulierungen werden in eine Programmiersprache übertragen. Nach der Verifizierung (siehe Hommen 1997), das heißt nachdem festgestellt wurde, daß das Programm keine Programmierfehler enthält und auf entsprechende Eingaben mit den entsprechenden Ausgaben reagiert, erhält man ein Programm, das für das konzeptionelle Modell bei entsprechender Parametrierung Ergebnisse liefert, die mit den Werten des Modellökosystems verglichen werden können. Abb. 4 zeigt den Ablauf von der Konzepterstellung bis zur Simulation.

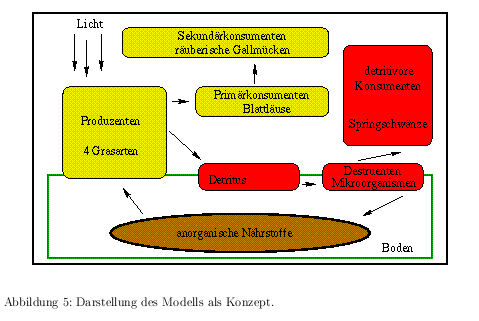
In einem konzeptionellen Modell werden die Eigenschaften und das Verhalten von Systemen durch logische Beschreibungen der Beziehungen so dargestellt, daß aus ihm heraus das mathematische Modell entwickelt werden kann. Dabei wird das Modell relativ grob gehalten und meist noch keine quantitativen Aussagen getroffen. In der Ökologie trifft man hier häufig Zeichnungen an, die die Interaktionen der in einem Modellökosystem betrachteten Populationen beschreiben. Sie veranschaulichen meist die Nahrungskette und zeigen bestimmte Eigenschaften auf, die auf das Modellökosystem einwirken und dieses dadurch verändern (Störgrößen). Diese konzeptionellen Modelle entsprechen häufig den graphischen Darstellungen der Modellökosysteme. Für das hier betrachtete Modellökosystem ist das Konzept in Abb. 5 dargestellt.
Die in Kapitel 3.1.1 beschriebenen Zusammenhänge müssen nun quantitativ beschrieben werden. Dabei können die Zusammenhänge sowohl in Form von mathematischen Gleichungen als auch durch logische Beschreibungen ausgedrückt werden. Eine in letzter Zeit häufig benutzte Art der logischen Beschreibung ist der Individuen-Ansatz (Dewdney 1987, Dewdney 1989). Hier wird der zeitliche Ablauf zum Beispiel einer Populationsentwicklung auf das einzelne Individuum fokussiert. Für jede Zeiteinheit des Modells werden alle Stadien des Organismus berechnet, wobei auch die Einflüsse der Umwelt beachtet werden. Dieses Verfahren ermöglicht eine anschauliche und detailierte Abbildung der Populationsdynamik auf der Basis des Verhaltens bzw. der Entwicklung jedes einzelnen Individuums. Der Individuenansatz verlangt dadurch sowohl viel Speicherkapazität als auch Rechenzeit. Zudem erfordert diese Methode detaillierte Kenntnisse oder Vorstellungen von den Zusammenhängen des Systems. Sie eignet sich deshalb für Organismen, deren Lebenszyklus genau bekannt ist und deren Population sich in einem überschaubaren Rahmen bewegt. Sie bietet aber auch eine Chance, die Vorgänge in einem Simulationsmodell detaillierter beschreiben zu können und gleichzeitig Simulationsergebnisse zu erhalten, die die Verhältnisse im Modellökosystem besser treffen als eine Beschreibung über Gleichungen (Dewdney 1987). Im folgenden wird das entwickelte Modell detailierter beschrieben und zusammenfassend mit Hilfe eines Struktogrammes erläutert.
Bei dem zu simulierenden Modellökosystem liegt das Hauptaugenmerk auf den Gallmücken als Endglied der Nahrungskette. Dabei interessieren sowohl die Auswirkungen der Chemikalie auf die Gesamtpopulation als auch der Verlauf der Populationsentwicklung der Blattläuse im Bezug auf die Anzahl der Gallmückenlarven. Entsprechend dieser Zielsetzung wurden die Modellierungsansätze ausgewählt.
Für die Gallmückenpopulation bietet sich der Individuenansatz an. Er ermöglicht die Berechnung der Anzahl an Eiern, Larven, Puppen und Imagines an beliebigen Simulationstagen. Da der Lebenszyklus der Gallmücke bekannt ist und viele Literaturwerte zur Verfügung stehen, ist die wichtigste Bedingung zur Anwendung des Individuenansatzes erfüllt. Desweiteren liegt die zu erwartende Populationsgröße in einem Bereich, für den die Rechenkapazität ausreichend ist.
Die Populationsgröße der Blattläuse liegt zum einen durch die große Anzahl an eingesetzten Tieren und zum anderen durch ihre hohe Vermehrungsrate weit über der der Gallmücken. Die Rechnerkapazität läßt hier einen Individuenansatz nicht zu. Eine Lösung bietet die Modellierung mit Hilfe einer Differentialgleichung auf der Grundlage des logistischen Wachstums. Hier wird über die Wachstumsrate der Blattläuse eine Populationsgröße N zum Zeitpunkt t berechnet. Damit läßt sich die Gesamtpopulationgröße für jeden Simulationszeitpunkt berechnen. Informationen über Larven und Imagines können aber nicht geliefert werden, sie sind für die Fragestellung hier aber auch nicht nötig.
Die Modellierung der Gräser erfolgt, analog der der Battläuse, mit einer Differentialgleichung, wobei die vier Grasarten als ein einheitliches Gras betrachtet wurden und der Mittelwert der Wachstumsraten der einzelnen Arten benutzt wurde.
Der Lebenszyklus der Gallmücken wurde häufig untersucht und ist im Kapitel 2 beschrieben. Um ihn im Individuenansatz zu formulieren, wurde für jeden Tag der Simulation der Zustand des Individuums berechnet. Somit durchläuft jede einzelne Gallmücke alle Stadien des Lebenszyklus von der Geburt bis zum Tod. Eine Ausnahme bildet dabei nur die Stammpopulation, die beim Start der Simulation vorhanden ist. Diese Individuen bekommen alle Eigenschaften zugewiesen, die nötig sind, um das gesamte Leben der Gallmücke im Modell zu beschreiben (siehe Tab. 3).
| Geschlecht | Männchen oder Weibchen |
| Alter | Alter der Gallmücke in Tagen |
| Stadium | Stadium, in dem sich die Gallmücke befindet |
| Sterbetag | Erreichbares Alter |
| Anzahl Eier | Anzahl der Nachkommen bei einem Weibchen |
| Eiablagetag | Tag im Leben der Gallmücke an dem Eier abgelegt werden |
| Eistadiumdauer | Dauer des Stadiums Ei |
| Larvenstadiumdauer | Dauer des Stadiums Larve |
| Puppenstadiumdauer | Dauer des Stadiums Puppe |
| Beutebedarf | Bedarf an Beutetieren bis zur Verpuppung |
| Fraß | Schon erbeutete Blattläuse bis zur Verpuppung |
| Hungertage | Anzahl Tage, die die Larve hungern kann |
| Kopulationstag | Tag im Leben der weibl. Gallmücke an dem Befruchtung |
| Toxitität | Zugehörigkeit zu dem Teil der Population, der in Folge der Chemikalienbelastung stirbt ( Dosis Letalis erreicht) |
| Generation | Zahl der Generationen nach der Stammpopulation |
Bei der Geburt werden den Zustandsgrößen und Parametern der betreffenden Gallmücken sinnvolle Werte zugewiesen. Die Parameter entstammen der Literatur und sind in der Regel Intervalle, wobei die Bandbreite der Intervalle über das Programm verändert werden kann. So lassen sich zum Beispiel neue Erkenntnisse leicht in die Simulation integrieren. Um die natürliche Schwankung der Werte nachzubilden, wird eine Zufallsfunktion eingesetzt. Diese Funktion ermittelt einen zufälligen Wert aus dem Intervall, wobei eine gleichmäßige Verteilung angenommen wird. Dadurch ist es möglich, daß es nicht nur immer identische Individuen gibt, sondern - wie in der Realität - unterschiedliche Gallmücken. Die in den folgenden Ausführungen beschriebenen Werte sind Standardeinstellungen, die der Simulation zugrundeliegen. Sie liefern auch die Ergebnisse, die die Grundlage des Vergleiches mit den praktischen Werten bilden.
Eine erwachsene Gallmücke legt zwischen dem ersten und dem dritten Tag des Imago-Stadiums 30 bis 40 Eier. Aus den Eiern entwickeln sich nach 2 bis 3 Tagen Larven. Gerade geschlüpfte Larven reagieren sehr stark auf eine Chemikalienbelastung, dabei hängt die Stärke der Reaktion zum einen von der Chemikalie selber als auch von deren Konzentration ab. Um die Sterblichkeit der Gallmücken in Abhängigkeit von der Chemikalienkonzentration abzubilden, muß eine entsprechende Modellökosystem-Versuchsreihe durchgeführt werden. Dabei wird ermittelt, wieviele Tiere bei einer bestimmten Chemiekalienkonzentration überleben, bezogen auf ein unbelastetes System. Trägt man die Ergebnisse graphisch auf, so erhält man eine Sterblichkeitsfunktion in Abhängigkeit von der Chemikalienapplikationsmenge (Dosis-Wirkungs-Funktion).
Um diese Funktion in der Simulation zur Verfügung zu haben, könnte zum einem aus der grapischen Funktion ein Polynom n-ten Grades bestimmt werden, mit dessen Hilfe sich dann zu jeder Applikationsmenge eine Sterblichkeit ermitteln läßt. Diese Funktion wird in die Simulation eingebaut. Zur Bestimmung dieses Polynoms stehen diverse Programme zur Verfügung, so daß sich der Rechenaufwand in Grenzen hält. Der Nachteil dieser Variante besteht darin, daß es sich bei der ermittelten Gleichung um eine diskrete Funktion (nur für genau dieses eine Problem gültig) handelt. So müßte für jede Chemikalie eine eigene Funktionsgleichung bestimmt werden, die aber einmal implementiert nicht mehr geändert werden kann. Somit müßte nicht nur bei jedem Chemikalienwechsel die Simulation neu programmiert werden, auch eine Änderung der Werte für eine bereits implementierte Substanz, aufgrund z.B. einer erhöhten Grundgesamtheit, zieht eine Änderung am Simulationsquellcode nach sich. Ein anderer Ansatz ergibt sich, wenn die Dosis-Wirkungs-Funktion mit einem sigmoiden Verlauf und einem Zeitverhalten 3. Ordnung angenommen wird. Das heißt, die Funktion kann eine Totzeit aufweisen, welche dem Bereich der Funktion (niedrige Konzentration) entspricht, in der ein Organismus nicht auf eine Chemikalie reagiert. Wird eine solche Gleichung implementiert, wobei die Koeffizienten der Gleichung zur Laufzeit der Simulation verändert werden können, braucht der Modellierer nur die Koeffizienten der, aus den Versuchen hergeleiteten, Dosis-Wirkungs-Funktion bestimmen und diese innerhalb der Simulation angeben. Somit müßte eine Simulation bei Änderungen der Dosis-Wirkungs-Funktion nicht neu übersetzt werden.
Der Umgang mit solchen Differentialgleichungen ist aber nicht ganz einfach. Schön wäre es, könnte die Mathematik zur Umsetzung der Dosis-Wirkungs-Funktion vom Rechner bereitgestellt werden. So könnte man sich vorstellen, daß die Ergebnisse einer Toxizitätsstudienuntersuchung vom Experimentator graphisch aufgetragen, und mit Hilfe eines Kurvenlineals oder einer Ausgleichsrechnung ein Kurvenverlauf bestimmt wird. Die Kurve wird anhand von Koordinatenpunkten in tabellarischer Form beschrieben und diese Tabelle dem Simulationsrechner zur Verfügung gestellt. Der Rechner konstruiert daraus wiederum einen glatten Kurvenzug innerhalb der Simulation. Somit muß der Modellierer nur noch seine ermittelte Dosis-Wirkungskurve angeben. Änderungen an dieser Stelle könnten jederzeit ohne erneute Übersetzung des Programmes berücksichtigt werden. Desweiteren ergibt sich auch der Vorteil, daß nicht nur S-Kurven hinterlegt werden könnten, sondern auch beliebige Kurvenverläufe, solange sie in x-Richtung streng monoton steigend sind (siehe unten).
Durch den Einsatz von kubischen Splines (Polynomzügen) kann diese Funktionalität erreicht werden. Die mathematischen Grundlagen werden weiter unten im Kapitel \ref{splinefunktion} gezeigt. Das Simulationsmodell benötigt nur noch die mit wenig bis gar keinem mathematischem Aufwand aufbereiteten Versuchsergebnisse der Toxizitätsstudie als Tabelle. Eine neue Tabelle kann somit eine andere Chemikalie darstellen, für die das Simulationsmodell dann, ohne daß sie geändert werden muß, neue Ergebnisse liefert. Da dieser Vorteil den Nachteil der komplexeren Implementation überwiegt, kommen die Splines zum Einsatz. Die im Pflanzenschutz eingesetzten Chemikalien sind in der Regel leicht flüchtige Substanzen. Im Hinblick auf diese Tatsache wird angenommen, daß mit der Zeit die Wirkung der Chemikalien auf die betroffenen Organismen abnimmt. Um dieser Eigenschaft Rechnung zu tragen, wird bei der Simulation angenommen, daß die aufgebrachte Chemikalie nur auf die erste Generation (F1) an Nachkommen der ,,Start'' Gallmücken wirkt, und die nachfolgenden Generationen keinen schädlichen Auswirkungen unterliegen.
Für eine bestimmte Chemikalie wird mit Hilfe der Splinefunktion eine Dosis-Wirkungs\-be\-zieh\-ung ermittelt. Gehört die Larve zu dem Teil der Population, die eine Chemikalienapplikation nicht überleben würde, so wird sie markiert und stirbt am nächsten Simulationstag. Welchem Populationsteil die Larve angehört, wird über eine Zufallsfunktion ermittelt, die Werte zwischen 0 und 100 liefert. Voraussetzung ist, daß die Funktion gleichverteilte Zufallswerte liefert. Eine Wirkung der Chemikalie auf die Eier, Puppen oder Imagines wird in der Simulation bisher nicht berücksichtigt.
Während des Larvenstadiums frißt eine Larve etwa 30 Blattläuse. Dabei ist zu beobachten, daß eine junge Larve pro Tag weniger Blattläuse frißt als eine Larve kurz vor der Verpuppung. Diesem Umstand wird dadurch Rechnung getragen, daß der Beutebedarf proportional zum Alter ansteigt. In der Simulation wird eine lineare Beziehung angenommen, deren Steigung abhängig von der Dauer des Larvenstadiums entweder z = 2 oder 3 beträgt. Es ergibt sich damit die Gleichung für den Fraß
| (1) |
Somit kommt jede Larve auf 30 zu fressende Blattläuse. Stehen nicht mehr ausreichend Beutetiere zur Verfügung, so kann die Gallmücke auch eine kurze Zeit mit weniger oder ohne Nahrung überleben. Dabei darf die Larve nicht jünger als drei Tage sein. Findet sie in dieser Zeit nicht ausreichend Nahrung, so stirbt sie. Ist die Larve älter, so überlebt sie die Tage der Nahrungsknappheit. Hungert die Larve, so wird vom Programm die Dauer des Larvenstadiums um die Anzahl an gehungerten Tagen verlängert. Ist nach Ablauf der Hungertage das Nahrungsangebot immer noch nicht ausreichend genug, so stirbt die Larve. Überlebt die Gallmücke das Larvenstadium, so kommt sie in das Puppenstadium, in der sie zwischen 12 bis 15 Tage verweilt. Danach wird sie zum Imago.
Bei den Imagines muß zwischen den Geschlechtern unterschieden werden, wobei die männliche Gallmücke im Modell nur altert. Erreicht sie das in den Eigenschaften festgelegte Höchstalter, so stirbt sie. Das Weibchen hingegen kann, wie oben erwähnt, zwischen 30 bis 40 Eier ablegen, dabei wird angenommen, daß alle Weibchen befruchtet werden. Der Zeitpunkt der Eiablage wird wieder durch die Eigenschaften festgelegt. Dabei kann es vorkommen, daß das Höchstalter der Gallmücke kleiner ist als der Zeitpunkt der Eiablage. In solch einem Fall stirbt die Gallmücke, bevor sie Eier ablegt. Somit läßt sich simulieren, daß nicht jedes fruchtbare weibliche Imago auch Nachkommen hat.
Kommt es zu einer Eiablage, so wird von der Simulation ein neues Individuum angelegt. Dabei wird jeder Eigenschaft aus der Tab. \ref{Gallmeigenschaften} ein neuer Wert zugeordnet. Eine Ausnahme bildet dabei die Eigenschaft ''Generation''. Dieser Wert wird vom der Mutter auf die Eier weitergegeben und um eins erhöht. Danach beginnt der Lebenszyklus von vorn.
Einen Überblick über die verschiedenen Zeiträume der Gallmückenentwicklung, die der Simulation zugrundeliegen, zeigt die Tab. 4.
| Lebensstadium | Dauer bei konst. 20°C |
|---|---|
| Ei | 2 - 3 d |
| Larve | 4 - 5 d |
| Puppe | 12 - 15 d |
| Imago weibl. | 4 - 5 d |
| Imago männl. | 2 - 3 d |
| Gesamt Lebensdauer männlich: | 20 - 26 d |
| Gesamt Lebensdauer weiblich: | 22 - 28 d |
Für die Simulation der Blattläuse muß die Populationsdynamik mathematisch beschrieben werden. Generell läßt sich das momentane Wachstum einer Population durch die Gleichung
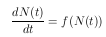
| (2) |
beschreiben. Sie sagt aus, daß die zeitliche Änderung der Populationsgröße dN/dt durch die Individuenzahl N(t) bestimmt wird. Die Funktion f(N) wird auch als Gesamtwachstumsrate einer Population bezeichnet. Sie beinhaltet alle Veränderungen einer Population, wie zum Beispiel das Sterben, die Geburten, die Immigration und die Emigration. Wird angenommen, daß das Wachstum eine direkte Funktion von N ist, und wird weiter angenommen, daß keine weiteren Faktoren auf die Wachstumsrate r einwirken, so ergibt sich
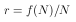
| (3) |
und Gleichung 2 wird zu
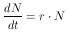
| (4) |
Die Gleichung 4 beschreibt exponentielles Wachstum und gilt also für dichteunabhängiges Populationswachstum. Ein unbegrenztes Wachstum ist aber nur über beschränkte Zeit möglich, da über kurz oder lang ein Faktor das Wachstum limitieren wird. Also muß ein dichteabhängiges Wachstum angenommen werden und somit r eine Funktion von N sein. Damit wird Gleichung 4 zu
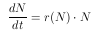
| (5) |
Dabei wird in der Realität beobachtet, daß die Populationsgröße N einem oberen Limit K, im weiteren auch Kapazität genannt, entgegenstrebt. Somit muß also angenommen werden, daß die Wachstumsrate r kleiner wird, je größer die Populationsgröße N ist. Ist die Kapazität K erreicht, so ist das Wachstum Null. Dabei wären verschiedene Verhalten für die Abnahme der Wachstumsrate denkbar. Eine einfache Annahme ist ein lineares Verhalten zwischen der Populationsgröße N und der Wachstumsrate r. Dieser Zusammenhang kann durch die Geradengleichung
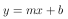
| (6) |
beschrieben werden. Wenn also r eine Funktion von N ist, ergibt sich aus Gleichung 6
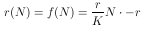
| (7) |
Wird diese Gleichung in Gleichung 5 eingesetzt, so ergibt sich
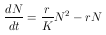
| (8) |
Diese Gleichung ist eine Form der Logistischen Verhulst-Gleichung, benannt nach Verhulst, der sie 1838 erstmals veröffentlicht hat. Durch Umformung erhält man die am meisten gebräuchliche Form
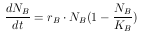
| (9) |
Betrachtet man Gleichung 9, so zeigt sich, daß bei
N<<K der Ausdruck 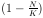 nahe 1 ist, und damit
das exponentielle Wachstum der Gleichung 4 erhalten bleibt.
Ist aber N = K so wird der Ausdruck Null, und damit auch die Wachstumsrate.
Die Funktion nähert sich also asymptotisch der Kapazität K. Damit läßt sich die
Populationsentwicklung in vielen Fällen hinreichend genau beschreiben.
nahe 1 ist, und damit
das exponentielle Wachstum der Gleichung 4 erhalten bleibt.
Ist aber N = K so wird der Ausdruck Null, und damit auch die Wachstumsrate.
Die Funktion nähert sich also asymptotisch der Kapazität K. Damit läßt sich die
Populationsentwicklung in vielen Fällen hinreichend genau beschreiben.
Mit der Gleichung 9 wird in der Blattlaussimulation die
Populationsgröße N bestimmt, indem für jede Simulationszeiteinheit
die vorangegangenen 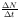 zum Startwert N0 addiert werden.
Das damit berechnete N ergibt dann das N0 für die nächste Zeiteinheit.
Somit erhält man nicht nur die aktuelle Gesamtpopulationsgröße, sondern auch
den effektiven Zuwachs an Individuen des aktuellen Zeitraumes.
zum Startwert N0 addiert werden.
Das damit berechnete N ergibt dann das N0 für die nächste Zeiteinheit.
Somit erhält man nicht nur die aktuelle Gesamtpopulationsgröße, sondern auch
den effektiven Zuwachs an Individuen des aktuellen Zeitraumes.
Wie auch bei den Gallmücken wirkt eine in der Umgebung der Blattläuse befindliche Chemikalie auf den Organismus. Die Reaktion der Blattläuse, zum Beispiel durch Infertilität oder Tod, wird analog der Vorgehensweise bei den Gallmücken durch eine Sterblichkeitsfunktion ausgedruckt. Dabei werden die in Versuchsreihen ermittelten Werte für die Sterblichkeit der Blattläuse in Abhängigkeit der Chemikalienkonzentration in einer Tabelle zur Verfügung gestellt. Die Simulation errechnet unter Einsatz der Splinefunktion eine konkrete Anzahl an Blattläusen, die den Simulationszeitraum nicht überleben (vergl. Kapitel 3.3.4). Dabei wird der Wirkungsdauer der Chemikalie dadurch Rechnung getragen, daß der Simulation eine Chemikalienwirkungsdauer in Tagen ab dem Tag der Chemikalienapplikation vorgegeben werden kann. Nur innerhalb dieser Zeit wird die Anzahl an durch Chemikalien getöteten Blattläusen berechnet. Dieser ermittelte Wert wird von der Population N abgezogen, und somit ergibt sich die aktuelle Populationsgröße. Die Reduzierung der Populationsgröße durch den Fraß der Gallmücken erfolgt wie in Kapitel 3.2.2 beschrieben während der Berechnung der Gallmückenpopulation. Daraus ergibt sich, daß die Blattlauspopulation des betreffenden Zeitintervalls vor der Gallmückenpopulation berechnet werden muß.
Die für die Simulation benötigten Gallmücken-Parameter konnten zum größten Teil aus der Literatur oder der Dissertation von Weyers (in Vorbereitung) entnommen werden. Für einige Werte, wie die Wachstumsrate und die Kapazität der Blattläuse, konnten aber keine Daten in der Literatur gefunden werden. Sie wurden in eigenen Versuchen ermittelt. Dabei wurden die Ergebnisse der in Kapitel 2.1.4 beschriebenen Versuche zugrundegelegt. Die Wachstumsrate der Gräser wurde indirekt aus den Werten der Dissertation von Weyers bestimmt.
Auf Grund der vorliegenden Werte (Tab. 10 im Anhang), die bis zum 31. Tag des Versuchs noch vor dem Wendepunkt der sigmoiden Kurve liegen, wird angenommen, daß in diesem Zeitraum exponentielles Wachstum vorliegt, und somit auch weder Nahrungs- noch Raumkonkurrenz auftritt. Außerdem gibt es weder Immigration noch Emigration, da es sich um ein abgeschlossenes System handelt. Folglich sind die Reproduktionseigenschaften eines Individuums von der Populationsgröße N (Anzahl Blattläuse) in diesem Zeitraum unabhängig, d.h. die Geburten- und Sterberate ist dichteunabhängig. Es ergibt sich eine konstante Wachstumsrate r.
Die Gleichung 10 beschreibt die Änderung der Populationsgröße N zur Änderung der Zeit t.
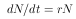
| (10) |
Setzt man nun als Startwert die Individuenzahl N0 zur Zeit t = 0, so ergibt sich
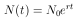
| (11) |
Um eine günstige graphische Darstellung zu erhalten, wird die Gleichung 11 logarithmiert und ln N(t) gegen t aufgetragen.
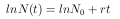
| (12) |
Daraus folgt, daß die Steigung der Kurve gleich der Wachstumsrate r ist.
Die Steigung wird ermittelt über ein Steigungsdreieck, mit
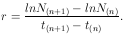
| (13) |
Aus den Versuchsergebnissen (Tab. 10 des Anhangs) ergibt sich der in Abb. 6 gezeigte Kurvenverlauf. Durch Anwendung von Gleichung 13 wird die Wachstumsrate r der Blattläuse bestimmt.
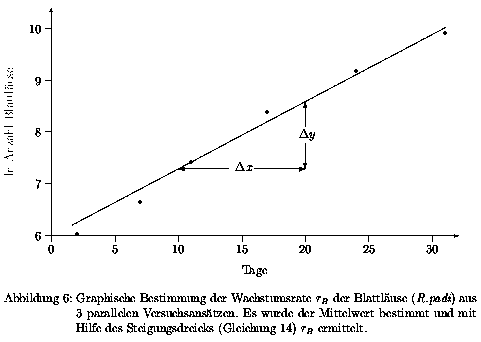
Sie ergibt sich zu
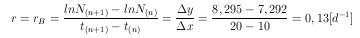
| (14) |
Diese Wachstumsrate rB wird in der Simulation als Standardwert benutzt, und dient auch als Basiswert für die Vergleichsrechnungen des Ergebnisteils und der Diskussion.
Häufig geht dieses exponentielle Wachstum in das logistische Wachstum über, das kurvenmäßig einem sigmoiden Verlauf entspricht. Am Wendepunkt der sigmoiden Kurve ist das Populationswachstum maximal. Die begrenzende Kapazität stellt sich infolge von Erschöpfung einer oder mehrerer Umweltressourcen ein, z.B. der Nahrung (vergl. Kapitel 3.2.3). Da in der Simulation mit der Verhulst-Gleichung (siehe Gleichung 9) gearbeitet wurde, mußte die Kapazität der Blattläuse für das Modellökosystem bestimmt werden. Dazu wurden die Ergebnisse des in Kapitel 2.1.4 beschrieben Versuchs graphisch aufgetragen. Diese Verlaufskurve der Blattlausanzahl in Abhängigkeit der Zeit (Abb. 7) zeigt, daß die Kapazität über den Versuchszeitraum noch nicht erreicht wurde. Der Kurvenverlauf läßt aber eine Extrapolation der Werte zu, so daß die Kapazität graphisch bestimmt werden kann.
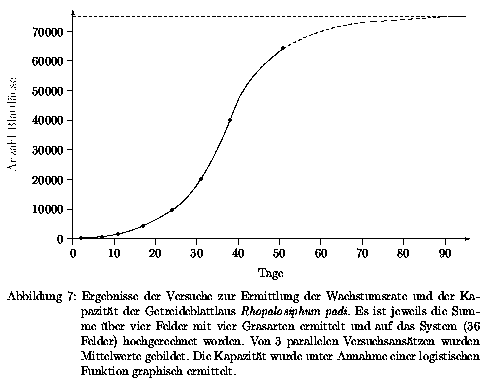
Aus dem Verlauf der Kurve in Abb. 7 ergibt sich eine Kapazität von 75000 Blattläusen pro System.
Die Populationsdynamik des Grases wurde ebenfalls mit der Verhulst Gleichung modelliert (siehe Kapitel 3.2.3) berechnet. Damit sind die dort erläuterten Gleichungen und Herleitungen auch hier gültig. Dabei muß aber beachtet werden, daß die Einheit für die Populationsgröße N nicht in Individuen, sondern in mg Trockengewicht angegeben wird. Die in der Simulation eingesetzte Gleichung berechnet das Trockengewicht demnach über die folgende Gleichung:
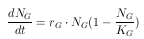
| (15) |
Auch bei den Gräsern wirkt eine Chemikalienbelastung in der Umwelt auf die Populationsgröße N. Um diese Wirkung zu erfassen, wird wieder die Splinefunktion eingesetzt. Mit ihrer Hilfe läßt sich der Prozentsatz der Population bestimmen, der bei einer diskreten Chemikalienkonzentration bezogen auf ein unbelastetes System abstirbt. Auch hier bilden die durch praktische Versuchsreihen ermittelten Werte die Grundlage der Splinefunktion. Dabei wurde die Wirkungsdauer der Chemikalie analog zu der Verfahrensweise bei den Blattläusen über die Chemikalienwirkungsdauer gesteuert. Damit erhält man am Ende dieser Berechnungen die aktuelle Populationsgröße N zum Zeitpunkt t.
Die vier Gräser wurden im Weiteren als eine Kenngröße Gras angesehen und folglich nur eine gemeinsame Wachstumsrate ermittelt. Zur Ermittlung dieser Wachstumsrate wurde der Zeitraum der Anzucht der Gräser ausgewählt. Die Versuchswerte stammen aus der Dissertation von Weyers (in Vorbereitung) und wurden analog der im Kapitel 3.2.3.1.1 beschriebenen Vorgehensweise bestimmt. In dem betrachteten Versuchszeitraum von 23 Tagen war noch kein Blattlausbesatz vorhanden. Die Versuchswerte (Tab. 11 im Anhang) wurden graphisch gegen die Zeit aufgetragen und mit Hilfe eines Steigungsdreieckes die Steigung bestimmt (Abb. 8).
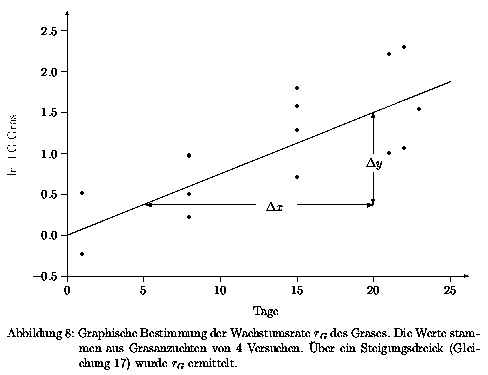
Wird die Gleichung 13 auf das Trockengewicht angewandt, so ergibt sich
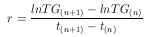
| (16) |
und aus Abb. 8 ergibt sich mit Gleichung 16 die Wachstumsrate der Gräser zu
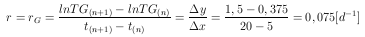
| (17) |
Anhand der Werte (Tab. 11 im Anhang) zeigt sich, daß eine Kapazität für
den Versuchszeitraum nicht erreicht wurde. Da die Simulation aber weiterhin
flexibel gestaltet werden sollte, wurde die Verhulst-Gleichung (9)
weiterhin angewendet und die Kapazität so groß gewählt, daß
der Ausdruck 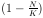 gegen Null strebt. Als Standard-Wert wurde
100.000 mg angesetzt.
gegen Null strebt. Als Standard-Wert wurde
100.000 mg angesetzt.
Um die Reaktion der Blattläuse und Gallmücken sowie der Gräser auf eine Chemikalie einer bestimmten Konzentration innerhalb der Simulation zu erfassen, sind entsprechende Kurvenverläufe zu bestimmen. Dabei müssen die Überlebensraten bezogen auf die Kontrollen gegen das Vielfache der Aufwandmenge aufgetragen werden (Tab. 12 im Anhang). In der Dissertation von Weyers (in Vorbereitung) wurde die Reaktion von Blattläusen, Gallmücken und Gräser auf die Chemikalie Trifluralin gemessen. Dabei wurde innerhalb einer Versuchsdurchführung für alle drei Organismen die entsprechende Reaktion bestimmt. Dadurch war allerdings auch eine Interaktion der Organismen untereinander gegeben. Diese Interaktionen wurden, falls nötig, so gut wie möglich herausgerechnet. Die entsprechende Bearbeitung und anschließende graphische Auftragung liefern die benötigten Kurvenverläufe.
In Anlehnung an die Diplomarbeit von Weyers (1994), die wesentliche Daten für die Verifikation der Simulation lieferte, wurde die Applikationsmenge als Vielfaches der praxisüblichen Anwenderkonzentration von 4,17 µl/ml ausgedrückt.
Als Kenngröße für die Wirkung der Chemikalie Trifluralin auf die Gallmücken wurde die Anzahl an Nachkommen der Gallmücken ausgewählt. Dabei wurden adulte befruchtete Weibchen in das Modellökosystem eingesetzt, das vorher mit der Chemikalie appliziert wurde. Die adulten Gallmücken der folgenden Generation wurden ausgezählt, und auf die entsprechende Anzahl Gallmücken der unbelasteten Systeme bezogen. Diese Verfahrensweise wurde mit diversen Vielfachen der Aufwandmenge durchgeführt. Die Ergebnisse sind in Abb. 9 dargestellt.
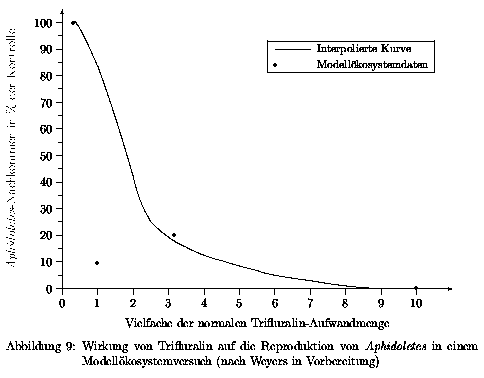
Die duch die ermittelten Werte konstruierte glatte Kurve wird als Wertetabelle 13 im Anhang gezeigt und der Simulation für die Anwendung der Splinefunktion hinterlegt.
Als Kenngröße für die Wirkung der Chemikalie Trifluralin auf die Blattläuse wurde die Gesamtgröße der Blattlauspopulation ausgewählt. Dabei wurden Blattläuse in das Modellökosystem eingesetzt und anschließend die Chemikalie appliziert. Danach wurden die Gallmücken in das System eingesetzt. Am Ende des Versuchszeitraumes wurde die Größe der Blattlauspopulation bestimmt und auf die entsprechende Größe der unbelasteten Systeme bezogen (Abb. 10).

Um den Einfluß der Gallmücken auf die Blattlauspopulation möglichst gering zu halten, wurde zur Populationsgröße die Anzahl Blattläuse hinzugerechnet, die von den überlebenden Gallmücken im Larvenstadium gefressen wurden.
Die durch die ermittelten Werte konstruierte glatte Kurve wird als Wertetabelle 14 im Anhang gezeigt und der Simulation für die Anwendung der Splinefunktion hinterlegt.
Als Kenngröße für die Wirkung der Chemikalie Trifluralin auf die Gräser wurde das Trockengewicht der Gräser ausgewählt. Dabei wurden Blattläuse in das Modellökosystem eingesetzt, und anschließend die Chemikalie appliziert. Danach wurden die Gallmücken in das System eingesetzt. Am Ende des Versuchszeitraumes ist das Trockengewicht der Gräser bestimmt und auf die entsprechende Größe der unbelasteten Systeme bezogen worden. Die Werte waren natürlich durch den Blattlausbesatz verfälscht, aber da angenommen wurde, daß die Blattläuse über den entsprechenden relativ kurzen Versuchszeitraum nur geringen Einfluß auf die Entwicklung der Gräser haben, wurde dieser Einfluß erst einmal vernachlässigt. Die Ergebnisse sind in Abb. 11 dargestellt.
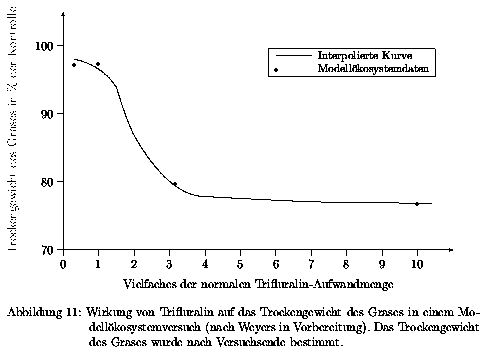
Die durch die ermittelten Werte konstruierte glatte Kurve wird als Wertetabelle 15 im Anhang gezeigt und der Simulation für die Anwendung der Splinefunktion hinterlegt.
Grundsätzlich ist die Modellierung von biologischen Vorgängen unabhängig von einer bestimmten Hardware oder Programmiersprache. Eine Ökosystemsimulation kann auf einer Workstation oder Mainframe genauso realisiert werden wie auf einem PC oder Kleinstrechner. Dabei ist nur zu beachten, daß je nach Komplexität der Aufgabe die Anforderungen an die Rechenleistung eines Computers wächst. So sollte, wenn man nicht Stunden oder gar Tage auf das Ergebnis der Simulation warten möchte, ein entsprechend schneller Rechner eingesetzt werden. Oft ist man aber auch an die vorhandene Hardware gebunden, so daß es vorkommt, daß eine komplexe Simulation doch auf einem leistungsschwachen PC oder Kleinstrechner realisiert werden muß. Häufig kommt es aber auch vor, daß ein altes Programm auf einen neuen Rechner übertragen werden soll.
Unter diesen Gesichtspunkten sollte, wenn eine neue Simulation entwickelt wird, eine moderne Programmiersprache eingesetzt werden, die für möglichst viele Rechnertypen und Betriebssystemen verfügbar ist. Dadurch ist es sehr leicht möglich, ein Programm von einem Rechner auf einen anderen zu portieren. Bei den graphischen Ausgaben ist die Auswahl noch schwieriger, da diese oft nicht nur an ein Betriebssystem, sondern sogar an eine Programmiersprache eines bestimmten Herstellers gebunden sind. Möchte man hier portierbar bleiben, müssen universelle Graphikbibliotheken eingesetzt werden.
Das Programm wurde in Standard C/C++ entwickelt, der zur Zeit modernsten Programmiersprache, die auch auf nahezu jedem Rechnertyp zur Verfügung steht. Für diese Programmiersprache gibt es eine Grafikbibliothek der Firma Sun, TCL/TK, die auf allen wichtigen Betriebssystemen eingesetzt werden kann. Durch diese Auswahl an Entwicklungswerkzeugen ist das Programm mit minimalem Aufwand auf fast alle heutigen Rechner portierbar. Somit kann sowohl eine Workstation unter UNIX als auch ein PC mit Windows als Betriebssystem eingesetzt werden. Als Entwicklungsrechner diente ein Pentium-PC unter Windows 95.
Die Randbedingungen legen das generelle Verhalten der Simulation fest. Diese Werte werden der Simulation als Startwerte mitgeteilt, noch bevor die ersten Berechnungen durchgeführt werden. Das wird durch eine sogenannte ,,Ini-Datei'' ermöglicht. Diese Datei enthält pro Zeile jeweils einen Wert, der jeweils einer bestimmten Variablen zugeordnet wird. Die Reihenfolge der Variablen ist dabei fest vorgeschrieben.
Zu diesen Randwerten zählen unter anderem die Simulationsdauer in Tagen und die Wirkungsdauer der Chemikalie auf die Gallmücken, die Blattläuse und die Gräser. Aber ebenso die Wachstumsraten für Blattlaus und Gras und der Tag der Chemikalienapplikation. Alle Randbedingungen sind in der Tab. 5 aufgeführt.
| Variable | Default Wert | Einheit |
|---|---|---|
| Minimum Nachkommen Gallmücke | 30 | [Individuen] |
| Maximum Nachkommen Gallmücke | 40 | [Individuen] |
| Minimum Eiablage Gallmücke | 1 | [d] |
| Maximum Eiablage Gallmücke | 3 | [d] |
| Minimum Lebensdauer weibl. Gallmücke (Startpopulation) | 4 | [d] |
| Maximum Lebensdauer weibl. Gallmücke (Startpopulation) | 5 | [d] |
| Minimum Lebensdauer männl. Gallmücke (Startpopulation) | 4 | [d] |
| Maximum Lebensdauer männl. Gallmücke (Startpopulation) | 5 | [d] |
| Alter der eingesetzten adulten Gallmücken | 22 | [d] |
| Dauer der Simulation | 60 | [d] |
| Startpopulationsgröße Anzahl der Blattläuse | 5000 | [Individuen] |
| Wachstumsrate r der Blattläuse | 0,130 | [d-1] |
| Kapazität KB der Blattläuse | 75000 | [Individuen] |
| Startwert der Gräser | 700 | [mg TG] |
| Wachstumsrate rG der Gräser | 0.075 | [d-1] |
| Kapazität KG der Gräser | 100000 | [Individuen] |
| Minimum Dauer Eistadium Gallmücken | 2 | [d] |
| Maximum Dauer Eistadium Gallmücken | 3 | [d] |
| Minimum Dauer Larvenstadium Gallmücken | 4 | [d] |
| Maximum Dauer Larvenstadium Gallmücken | 5 | [d] |
| Fraßsteigerung beim 4-tägigen Larvenstadium | 3 | [Individuen/d] |
| Fraßsteigerung beim 5-tägigen Larvenstadium | 2 | [Individuen/d] |
| Minimum Dauer Puppenstadium Gallmücken | 12 | [d] |
| Maximum Dauer Puppenstadium Gallmücken | 15 | [d] |
| Minimum Lebensdauer weibl. Gallmücke | 4 | [d] |
| Maximum Lebensdauer weibl. Gallmücke | 5 | [d] |
| Minimum Lebensdauer männl. Gallmücke | 2 | [d] |
| Maximum Lebensdauer männl. Gallmücke | 3 | [d] |
| Minimum Anzahl Blattläuse, die immer überleben | 100 | [Individuen] |
| Maximale Hungertage einer Gallmückenlarve | 0 | [d] |
| Chemikalienbelastung (Chemikalienkonzentration) | 0 | [Applikationsmenge] |
| Wirkungsdauer der Chemikalie auf Blattläuse | 5 | [d] |
| Wirkungsdauer der Chemikalie auf Gräser | 5 | [d] |
Zum Teil lassen sich diese Randbedingungen über die graphische Bedienoberfläche der Simulation verändern, wie zum Beispiel die Simulationsdauer und die Chemikalienkonzentration. Die übrigen Bedingungen können über den ,,Ini-File'' der graphischen Oberfläche beeinflußt werden. Beim Start der Simulation wird als erstes diese Randbedingung aus der Initialisierungsdatei eingelesen.
Anschließend müssen bestimmte Parameter der Simulation vor dem Start der eigentlichen Berechnung auf einen Anfangswert gesetzt werden. So ist zum Beispiel die Matrix, in der später das Abbild der Gallmückenpopulation gespeichert wird, so zu verändern, daß keine Eier, Larven oder Puppen existieren. Diesen Arbeitsschritt nennt man Initalisierung. Er ist deshalb notwendig, weil beim ersten Anlegen einer solchen Matrix die vom Rechner vorbelegten Werte undefiniert sind (C++ typisches Verhalten).
Innerhalb dieser Initalisierung werden auch verschiedene andere Arbeiten durchgeführt, die nicht direkt zur Berechnung der Simulation gehören. Ihre Ausführung könnte auch erst im Zuge der eigentlichen Simulation erfolgen, erzielt aber im Vorfeld durchgeführt eine wesentliche Beschleunigung. Dazu zählt zum Beispiel die Initalisierung der Matrizen für die Spline-Funktion, die im Kapitel 3.3.4 beschrieben ist.
In den vorangegangenen Abschnitten wurden die Abläufe der einzelnen
Simulationsbereiche - Gallmücken, Blattläuse und Gräser -
ausführlich beschrieben. Dabei wurde schon
 erwähnt, daß für alle Bereiche die jeweilige
Populationsgröße in bestimmten Zeitabständen berechnet wird. Als sinnvolle
Zeiteinheit ist hier ein Tag
ausgewählt worden, da auch in den praktischen Versuchsreihen die Ergebnisse in
Tagesabständen gemessen wurden. Somit wurden also für jeden Tag die drei
Populationsgrößen bestimmt. Das zeitliche Zusammenspiel dieser drei Teilbereiche
muß noch aufeinander
abgestimmt werden. Maßgeblich für den zeitlichen Ablauf ist dabei die
Nahrungskette der drei Arten. Hier dienen die Gräser als Wirt für die
Blattläuse, die wiederum als Nahrungslieferant für die Gallmücken herangezogen
werden. Folglich mußte mit der Berechnung der Populationsgröße
des Grases gestartet werden, da diese in der Nahrungskette am Anfang steht.
Dabei wird davon ausgegangen, daß der Boden immer genügend Nährstoffe für eine
ungehemmte Entwicklung der Gräser zur Verfügung stellen kann. Der grobe
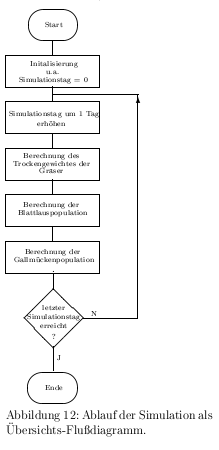
Ablauf der Simulation ist in Abb. \ref{fluss} gezeigt. Dabei wurden die
realisierten Interaktionen der Populationen in den Berechnungen der jeweiligen
Populationsgrößen berücksichtigt. Deren detailierter Ablauf wird in den
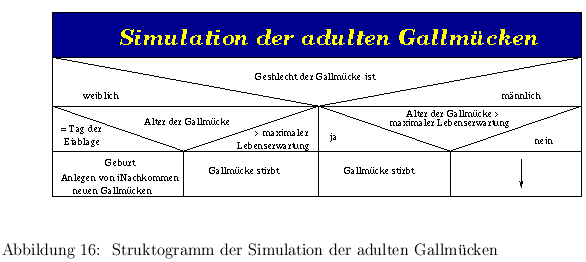
Abb. 13,14,15 und
16 als Struktogramm dargestellt.
erwähnt, daß für alle Bereiche die jeweilige
Populationsgröße in bestimmten Zeitabständen berechnet wird. Als sinnvolle
Zeiteinheit ist hier ein Tag
ausgewählt worden, da auch in den praktischen Versuchsreihen die Ergebnisse in
Tagesabständen gemessen wurden. Somit wurden also für jeden Tag die drei
Populationsgrößen bestimmt. Das zeitliche Zusammenspiel dieser drei Teilbereiche
muß noch aufeinander
abgestimmt werden. Maßgeblich für den zeitlichen Ablauf ist dabei die
Nahrungskette der drei Arten. Hier dienen die Gräser als Wirt für die
Blattläuse, die wiederum als Nahrungslieferant für die Gallmücken herangezogen
werden. Folglich mußte mit der Berechnung der Populationsgröße
des Grases gestartet werden, da diese in der Nahrungskette am Anfang steht.
Dabei wird davon ausgegangen, daß der Boden immer genügend Nährstoffe für eine
ungehemmte Entwicklung der Gräser zur Verfügung stellen kann. Der grobe
Ablauf der Simulation ist in Abb. \ref{fluss} gezeigt. Dabei wurden die
realisierten Interaktionen der Populationen in den Berechnungen der jeweiligen
Populationsgrößen berücksichtigt. Deren detailierter Ablauf wird in den
Abb. 13,14,15 und
16 als Struktogramm dargestellt.

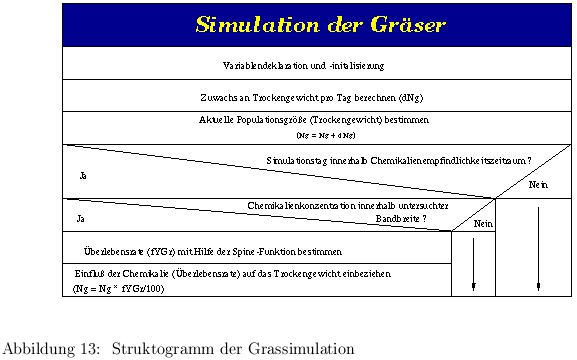
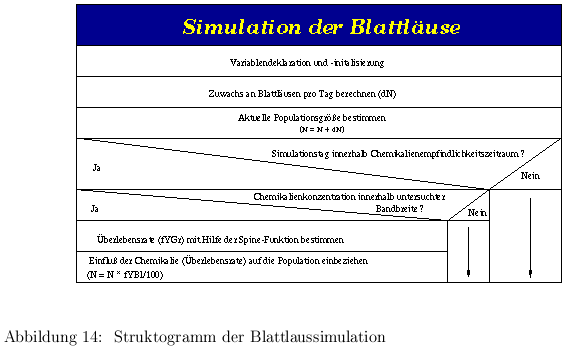


Abbildung 15: Struktogramm der Gallmückensimulation
Das im Modellökosystem eingesetzte Gras bestand aus vier Arten, die auch unterschiedlich stark von Blattläusen frequentiert wurden. Dabei konnte beobachtet werden, daß bei Nahrungsverknappung, als eine Grasart mehr unter den Blattläusen litt als die anderen, die Blattläuse zu einer anderen Grasart wechselten. Besonders auffällig war, daß Holcus erst wenn die anderen Grasarten schon geschwächt waren, für die Blattläuse interessant und somit erst verhältnismäßig spät dichter besiedelt wurde. Ein Grund dafür könnte die starke Behaarung der Pflanze sein. Hinzu kam, daß am Ende des Versuchszeitraumes trotz einer sehr hohen Blattlausdichte auf Holcus keine sichtbare Schädigung der Pflanze zu erkennen war. Damit ergeben sich sehr komplexe Zusammenhänge innerhalb der Blattlaussimulation. Da hierfür keine Daten zur Verfügung stehen, die zum einem die Wanderung der Blattläuse und zum anderen den Verlauf der Erholung der geschädigten Gräser beschreiben, und da das Hauptaugenmerk auf dem Verhalten der Gallmücken liegt, wird hier die Simulation vereinfacht. Dadurch, daß die vier Grasarten als eine einzelne Grassorte betrachtet wurden, ließ sich bei der Auswertung (siehe Kapitel 3.2.4.1) eine für alle Gräser gemeinsame Kapazität bestimmen. Eine Schädigung dieses ,,Universal''-Grases konnte durch die Robustheit von Holcus ausgeschlossen werden. Daher kann vereinfachend gesagt werden, daß die während der betrachteten Simulationszeiträume auftretenden Blattlauspopulationen sich unabhängig von der Graspopulationsgröße entwickeln, also immer ein ausreichendes Nahrungsangebot für die ungehinderte Entwicklung der Blattläuse zur Verfügung steht. Auf der anderen Seite wird das Wachstum und damit die Kapazität und die Wachstumsrate des Grases durch die Blattläuse nicht beeinflußt. Folglich kann die tägliche Änderung der Populationsgröße NG mit Hilfe der Gleichung 15 bestimmt werden.
Nachdem die Populationsgröße der Gräser bestimmt wurde, folgt als nächstes die Populationsgröße der Blattläuse. Diese kann erst einmal analog zum Vorgehen bei den Gräsern mit Hilfe der Gleichung 9 bestimmt werden. Hier müssen jedoch auch noch die Interaktionen zwischen Blattläusen und Gallmücken berücksichtigt werden. Wie schon im Kapitel 3.2.2 erwähnt, ist das Vorhandensein einer Mindestmenge an Blattläusen für die ungehinderte Entwicklung der Gallmückenlarven unbedingt erforderlich. Dieser Fraß muß der aktuellen Blattlauspopulation entzogen werden. Da die Anzahl an gefressenen Blattläusen abhängig von Anzahl und Alter der Gallmückenlarven ist, muß somit für jede Simulationszeiteinheit und jede Gallmückenlarve der Beutetierbedarf berechnet werden. Da sich diese Werte aber erst innerhalb der Gallmückensimulation ergeben, können sie auch erst dort berücksichtigt werden.
Bei der Simulation der Gallmücken wurde für jeden Tag das jeweilige Stadium jedes einzelnen Individuums neu berechnet. Dabei wurde wie im Kapitel 3.2.2 beschrieben vorgegangen und auch der Fraß der Gallmückenlarve ermittelt. Diese hier errechnete Anzahl an Blattläusen wurde sofort von der Blattlauspopulation abgezogen. Da dieses Vorgehen für jede Larve sequentiell geschieht, kann es vorkommen, daß der errechnete Bedarf an Blattläusen größer ist als deren Population. Wenn innerhalb der Simulation der errechnete Fraß dennoch von der Gesamtpopulation an Blattläusen abgezogen würde, würden die Blattläuse ganz aussterben. Dieses Verhalten ist aber nicht realistisch. Deshalb wurde ein Wert festgelegt, der angibt, wie hoch die Zahl der Blattläuse ist, die auf jeden Fall die Futtersuche der Gallmückenlarven überleben. Es ist aber durchaus möglich und auch gewollt, daß die Blattläuse durch eine Chemikalie ausgerottet werden können. Dieser Schwellenwert für die Blattläuse ist auch deshalb nötig, da es in der Natur den Gallmücken mit fallender Blattlausdichte immer schwerer fällt, ihre Beute zu finden. Um die Beutesuche in die Simulation einzubauen, müßte jede räumliche Position der Gallmücken und der Blattlaus berechnet und verwaltet werden. Das setzt aber voraus, daß die jeweiligen Simulationen als Individuenansätze angelegt wurden. Da aber die Blattlaussimulation nicht als Individuenansatz (vergl. Kapitel 3.2.2) durchgeführt wurde, kann auf die Beutesuche nicht eingegeangen werden. Fällt also der Wert der Blattlauspopulation unter den Schwellenwert, so muß die Gallmücke hungern.
Bei der Auswertung von Versuchsergebnissen stellt sich in den Naturwissenschaften häufig das Problem, daß zu einer Folge von ermittelten Werten eine Funktion bestimmt werden soll. Die klassische Mathematik liefert hier durch den Approximationssatz von Weierstraß einen Lösungsweg. Der Satz sagt aus, daß es möglich ist, jede sinnvolle Funktion mit Hilfe eines Polynoms (ausreichend hohen Grades) zu approximieren, es also für jede sinnvolle Funktion ein entsprechendes Polynom gibt. Aus den gegebenen Werten ist somit ein Interpolationspolynom n-ten Gerades zu ermitteln. Der Rechenaufwand für die Bestimmung eines solchen Polynoms ist enorm hoch. Da aber der Anwendungsfall so häufig vorkommt, gibt es diverse Programme, die aus gegebenen Wertepaaren das entsprechende Polynom bestimmen.
Der Nachteil dieser Vorgehensweise ist, wie in Kapitel 3.2.2 erwähnt, daß ein einmal bestimmtes Polynom nur für genau die zugrundeliegenden Werte gilt. Ändert sich aus irgendeinem Grund die Basis, so muß auch das Polynom neu bestimmt werden. Für eine Simulation muß daher beachtet werden, daß die Simulation bei Änderungen der Basis-Werte neu programmiert werden muß, wenn solche Polynome verwendet werden.
Sollen aber Bereiche simuliert werden, deren Werte veränderbar sind, so muß ein anderer Ansatz ausgewählt werden. In dem Fall der Gallmückensimulation zum Beispiel ist dieses bei der Reaktion der Gallmücken auf eine Chemikalienbelastung der Fall. Hier können genauere Untersuchungen neue Werte ergeben oder aber unterschiedliche Chemikalien eingesetzt werden. Um die Simulation flexibel zu gestalten, wurde daher die Spline-Interpolation angewandt.
Spline wird im Englischen ein Arbeitsgerät genannt, mit dessen Hilfe man ansprechende Kurven zeichnen kann. Dabei wird eine Anzahl Punkte fixiert und so mit einem Stück biegsamen Holz, Metall oder Plastik miteinander verbunden, daß ein glatter Kurvenzug entsteht, der abgezeichnet wird. Dabei zeigt sich, daß jedes Kurvenstück zwischen zwei Punkten durch ein Polynom dritten Grades der Form
beschrieben werden kann (Sedgewick 1990).
Bei den Spline löst man sich also von der Idee, ein einziges Polynom durch alle Punkte der Funktion zu legen. Vielmehr setzt man die gesuchte Kurve aus aneinandergereihten kubischen Polynomen zusammen, die mathematisch einfach zu handhaben sind. Dabei muß aber gewährleistet sein, daß die Punkte streng monoton angeordnet sind, also
gilt. Da die Polynomzüge eine glatte Kurve ergeben müssen, bedeutet das, daß keine Knicke und scharfe Biegungen auftreten dürfen. Mathematisch ausgedrückt bedeutet das, daß die erste Ableitung des Endpunktes des i-ten Intervalles gleich der ersten Ableitung des Startpunktes des i+1-ten Intervalles ist (gleiche Steigung). Aber auch die zweiten Ableitungen müssen übereinstimmen (gleiche Krümmung). Daraus folgt, daß die Polynomzüge zweimal stetig differenzierbar sein müssen. Ausnahmen bilden hier die Intervalle S1 und Sn, die entweder kein vorhergehendes bzw. nachfolgendes Intervall haben. Hier wird angenommen, daß s'(x1) = 0 und s''(xn) = 0, also die erste und die zweite Ableitung Null ist (Randbedingungen). Da x- und y-Werte gegeben sind, ergeben sich die folgenden Gleichungen
Dabei wird formal angenommen, daß sn(xn) = an, s''n(xn) = 2cn ist (Engeln-Müllges 1993), dazu kommen noch die zwei Randbedingungen. Man erhält also 4n+2 Bedingungen für die 4n+2 Koeffizienten ai, bi, ci, di. Dieses Gleichungssystem läßt sich mit Hilfe des Gauß-Algorithmus lösen. Das Gaußverfahren wurde nach den Beschreibungen von Leupold et al (1989), Engeln-Müllges (1993) und Sedgewick (1990) in das Simulationsprogramm eingebaut.
Eine Zufallsfunktion muß aus einem Intervall eine diskrete Zahl liefern, wobei aber gewährleistet ist, daß jede Zahl des Intervalls mit gleicher Wahrscheinlichkeit auftreten kann. Für diesen Anwendungsfall liefert die Sprache C/C++ die Standardfunktion rand, die Zufallswerte im Bereich von Null bis RAND_MAX (einer betriebssystemabhängigen Variable, meist 215-1) zur Verfügung stellt. Da diese Funktion mit Hilfe einer Zahlentafel arbeitet, kann man mit der Funktion srand einen Startwert für rand festlegen. Nach der Transformation des ermittelten Wertes auf das gerade benötigte Intervall erhält man die gesuchte Zufallszahl.
Um möglichst einfach an eine Zufallszahl zu gelangen, wurde eine eigene Funktion implementiert, die - ausgehend von den beiden Standardfunktionen rand und srand - eine Zufallszahl auf ein angegebenes Intervall abbildet.
In der Simulation kann nun diese Zufallsfunktion zum Beispiel dazu verwendet werden, um die Anzahl an Nachkommen einer Gallmücke zu bestimmen. Dazu muß die Funktion nur mit einem Minimum und einem Maximum an zu erwarteten Eiern aufgerufen werden. Sie wird aber auch zur Bestimmung der Zugehörigkeit einer Gallmücke zu einer Populationsgruppe während der Chemikalienbelastung benutzt.
Für den Fall der Toxizitätsstudie der Gallmücken wird von der Splinefunktion der Anteil an Gallmücken geliefert, die eine bestimmte Chemikalienkonzentration überleben. Dieser Wert ist in Prozent der Kontrolle angegeben. Die Simulation arbeitet aber bei den Gallmücken mit dem Individuenansatz. Somit kann nicht einfach die aktuelle Populationsgröße geteilt durch 100 und mit dem Wert der Splinekurve multipliziert werden, da die Populationsgröße zu diesem Zeitpunkt noch gar nicht bestimmt werden kann. Dies ist erst am Ende einer Simulationszeiteinheit möglich. Die Lösung besteht darin, daß mit Hilfe der Zufallsfunktion ein Zufallswert zwischen 0 und 100 ermittelt, und mit der Überlebensrate, die die Splinefunktion liefert, verglichen wurde. Ist der Zufallswert größer als die Überlebensrate, so stirbt die Gallmücke.